Beautiful Work Info About Can A Curve Be Straight Chartjs Dashed Line

I am trying to prove the following theorem.

Can a curve be straight. To understand why curved lines cannot become straight without changing their length, it's important to consider the fundamental properties of curves and straight lines. This is the definition that appeared more than 2000 years ago in euclid's elements: You can only speak about distances between points on the curve.

I think euler's formula of $ k_n=k_1cos^2(\theta)+k_2sin^2(\theta) $ may help but i'm not sure what the principal curvatures would be of a straight line. You can't decide whether to use a straight line or a curved line between data points because you have no data to tell you what the shape of the line should be. $$\epsilon_{d}=\frac{\delta{q}}{\delta{p}}\frac{p}{q}$$ the equation itself is non.

(forgot to mention this in the clip:. The [curved] line is […] the first species of quantity, which has only one dime… A curved line is defined as a line that is not straight but is bent.

In other words, a curve is defined as a group of points that resemble a straight line that. Ideally, it is smooth and continuous. A straight line is a curve with the equation ax + by + c = 0, or equivalently:

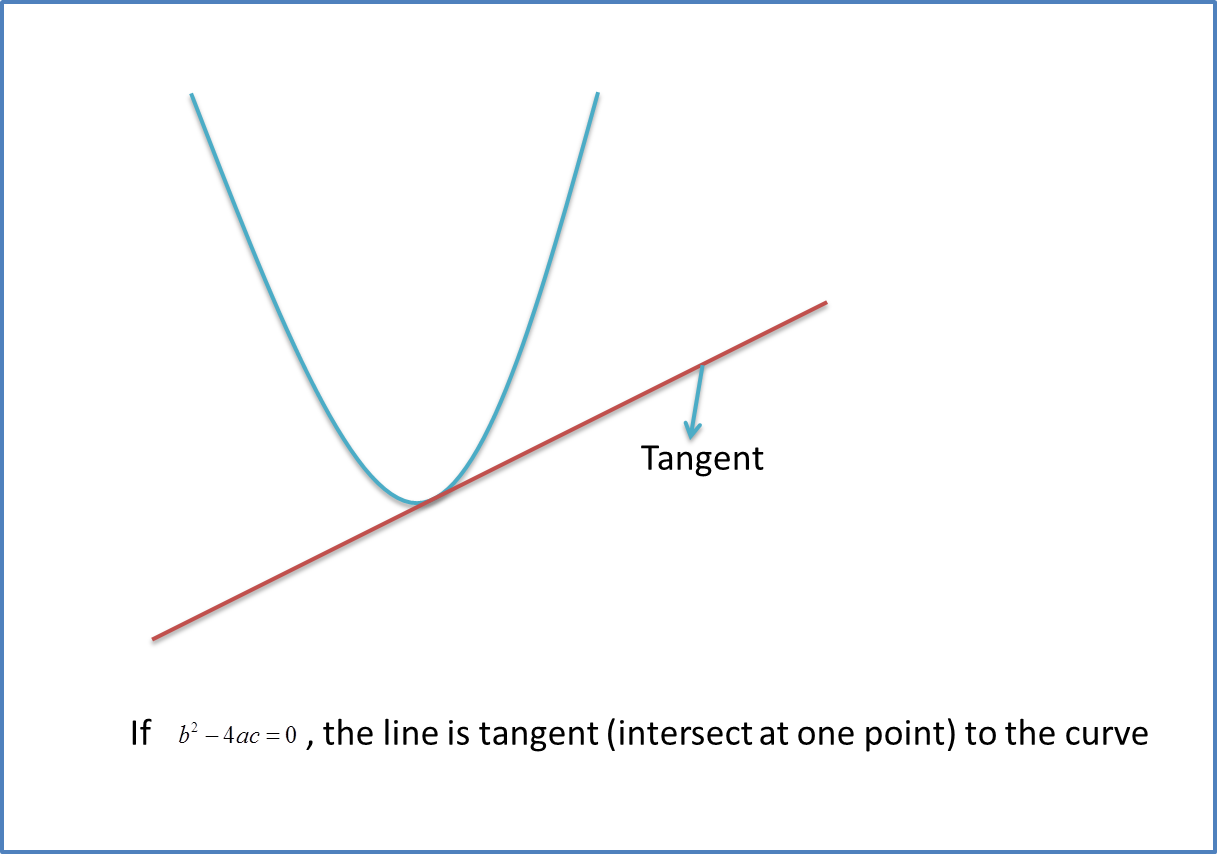
If κ = 0 κ = 0 is the curvature of γ γ, then γ(s) γ ( s) is a straight line. A curved line is one that is not straight and is bent. Y = ax + b (assuming the line isn't vertical).

A straight line is traced by a point moving in a direction that does not change. Take the equation for the elasticity of demand: An example of a curved straight line.

In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. You might think that you can have a fractal. There are a few examples where the fit is a curve or a straight line.

A curved line is sometimes called a curve. We know that the curvature of the straight line is zero. A curved line is a type of line that is not straight and is bent.

However, curves which are not everywhere differentiable do not have that property: Intuitively, a curve may be thought of as the trace left by a moving point. Now, can we draw a rectangle as a curve?

You may say, you need to use a straight ruler and protractor (for the right angles) and then lift the pen each. Yes, such curves exist. It is continuous and smooth, without any sharp turns.