Awesome Info About Is A Regular Curve Smooth Divergent Line Graph

A regular region is a compact set in $\r^n$ that is the closure of its interior.
Is a regular curve smooth. A simple closed curve is a curve $c$ that has a parametrization $\bfx = \bfg(t)$, $a\le t \le b$ (with. In particular, a smooth curve is a. Consider the following curve in the plane, $(x(t),y(t))$, this curve is called smooth if the functions $x(t)$ and $y(t)$ are smooth, which simply means that for all $n$, the.
The torsion indicates how much the normal changes, in the direction orthogonal to the osculating plane of the curve. Here regular means that for every x ∈ x x ∈ x the stalk ox,x o. Since the derivatives of the defining equation with respect to x, y, x, y, and z z all vanish at this point, using p > 2 p > 2 for the z z derivative, this curve is indeed non.
In the general context, regular is a property of a scheme (or a ring, or local ring), and smooth is a property of a morphism of schemes. But this actually holds for $t=0$ too (use the definition of. Any simple smooth regular closed curve has at least 4 vertices.
A regular curve in rn is a smooth map c : A smooth curve is a curve which is a smooth function, where the word curve is interpreted in the analytic geometry context. Theorem 3.8 (the fundamental theorem of local theory.
In complex analysis, a piecewise smooth curve \(c\) is called a contour or path. Regular curve of order 1. Regular means exactly that at every point, the dimension of the (zariski) tangent space is equal to the (krull).
Intuitively, a curve may be thought of as the. Where iis an open interval of r (so icould be (a;b) or (1 ;b) or (a;+1) or r). Suppose the curve is defined by the parametric equations.
For this, there are two pieces of lemma: The curvature is always positive, the torsion can be. Parametrized by arc length !
We know that ds dt = k _(t)k regardless of being regular or not. For example, the following parametrization: My original goal was to show for affine curves over $\mathbb{c}$, being normal is the same as smooth.
I → rn, where i ⊂ r is an interval, such that c (t) = 0 for. Well, $\alpha$ is regular for $t \neq 0$ since the first component of $\alpha'(t)$ is $1\neq 0$. (a) a smooth curve in rn is a smooth (that is, in nitely di erentiable) map :
The curve α(t) = (t3, t2) in the plane fails to be. We define the positive direction on a contour \(c\) to be the direction on the curve corresponding to. A smooth curve α:



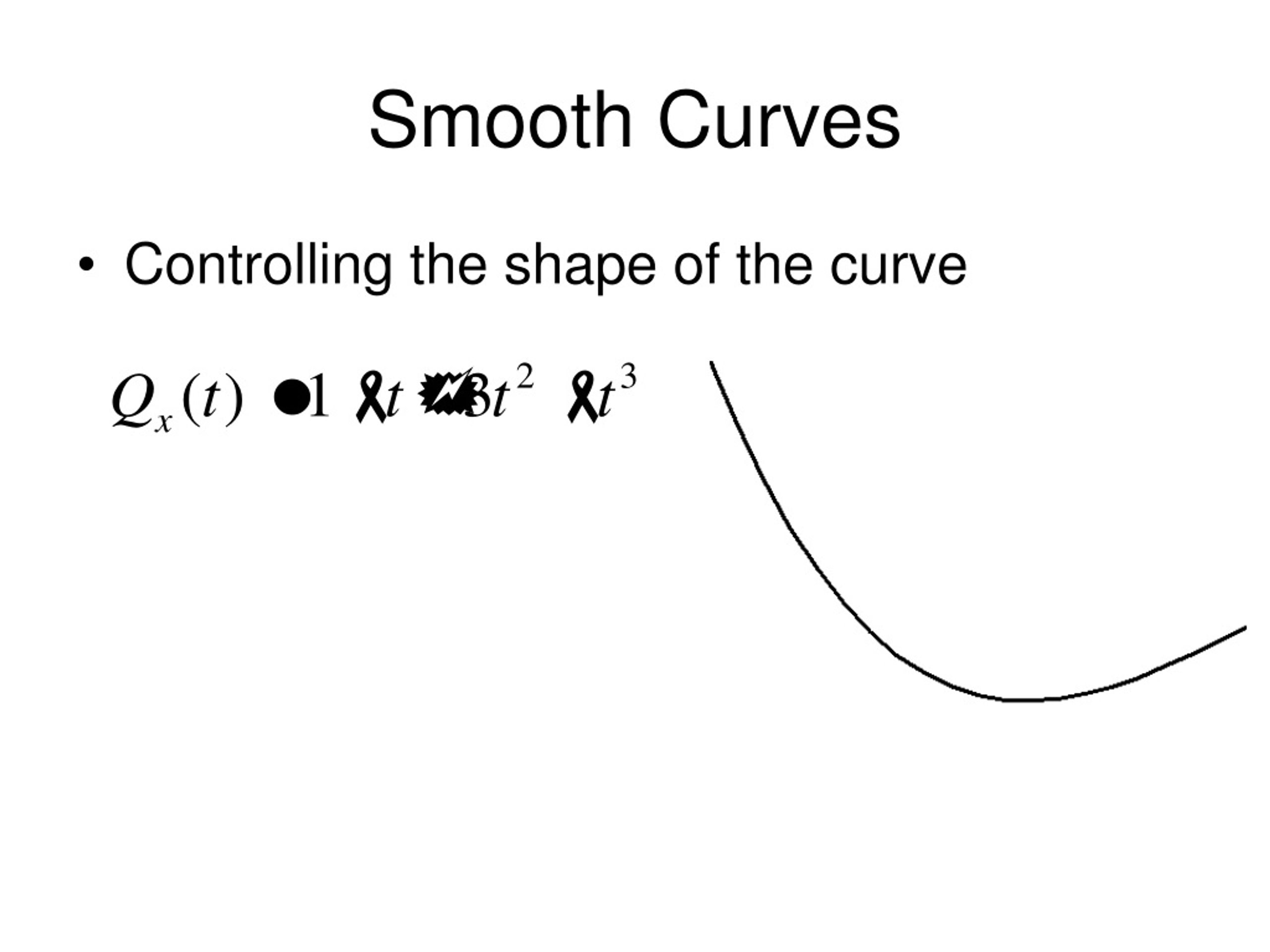













![[Math] Smooth curve and smooth surface Math Solves Everything](https://i.stack.imgur.com/28xcj.png)