Unbelievable Info About Why Is Curve Sketching Important In Real Life How To Create A Combo Chart Excel

Mean value theorem, antiderivatives and differential equa

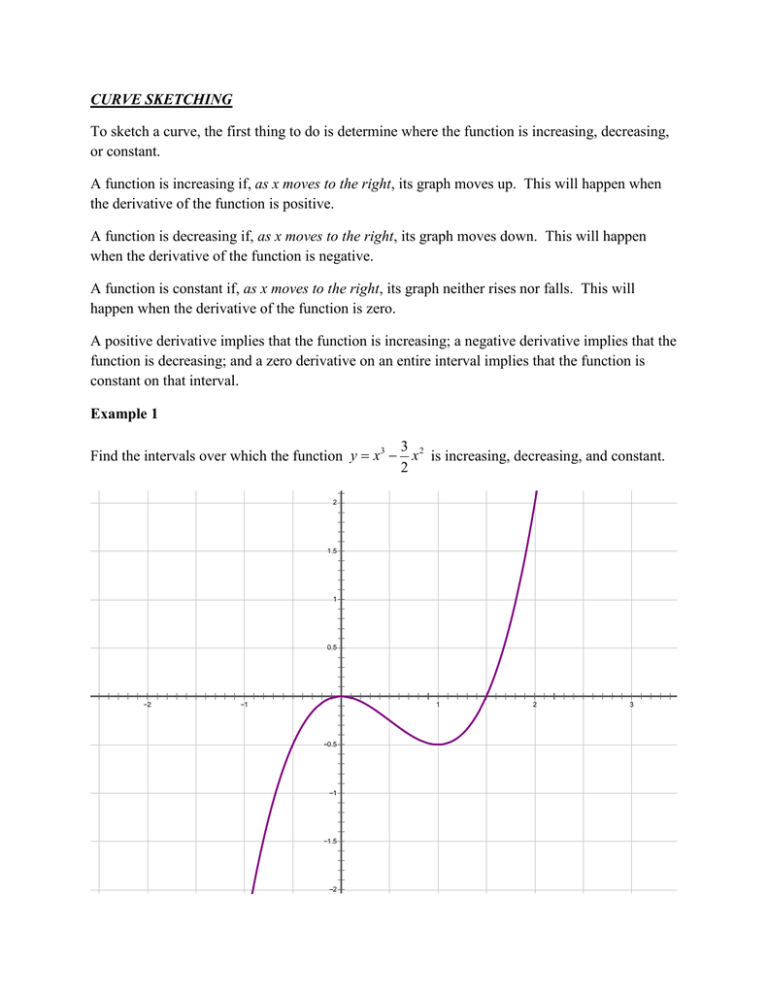
Why is curve sketching important in real life. The only critical numbers for \(f\) are \(x = 1\) and \(x = 3\), and they divide the real number line into three intervals: A function can increase between two points in different ways, as shown in figure [fig:concav3]. Find the domain of the function and.

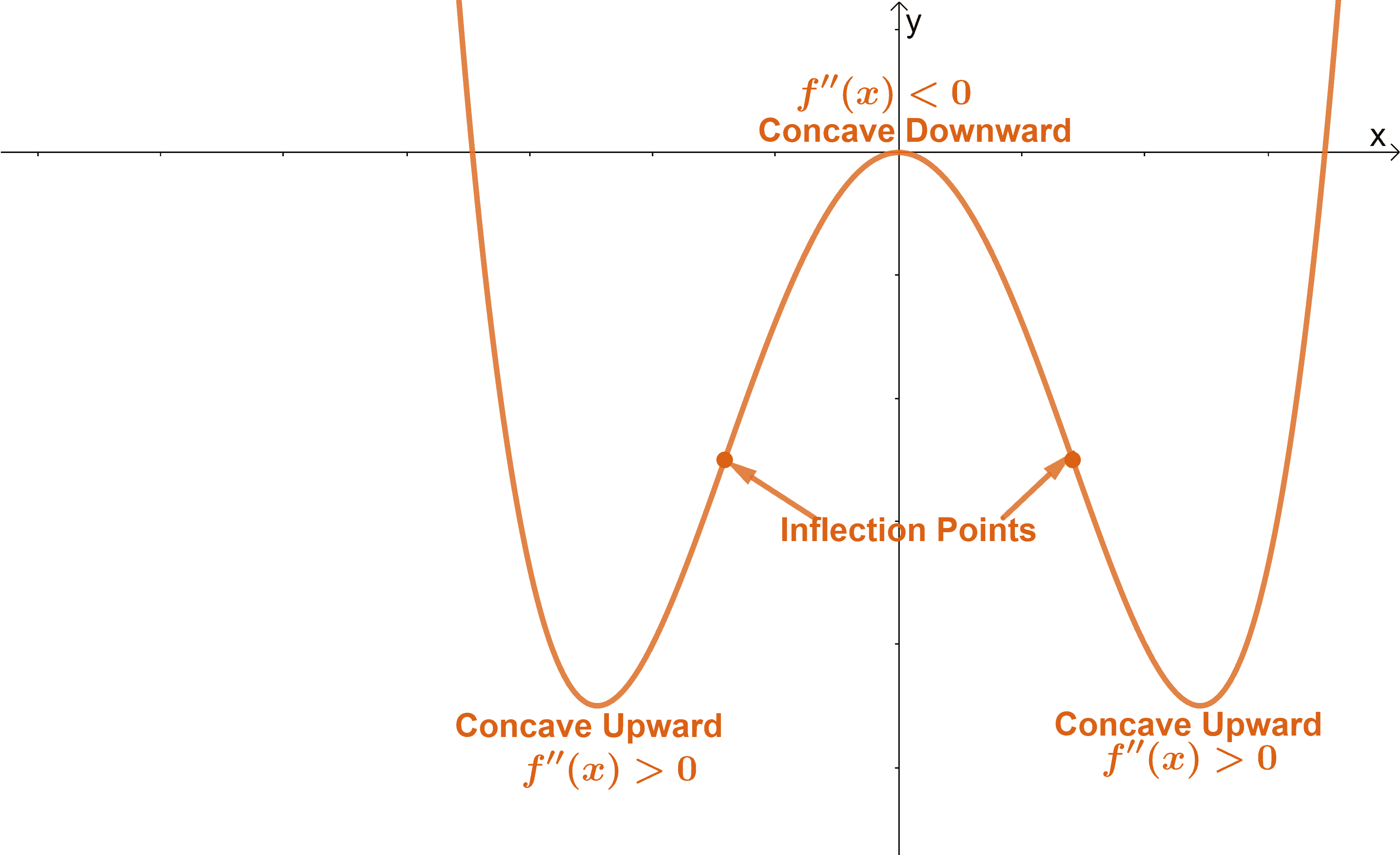
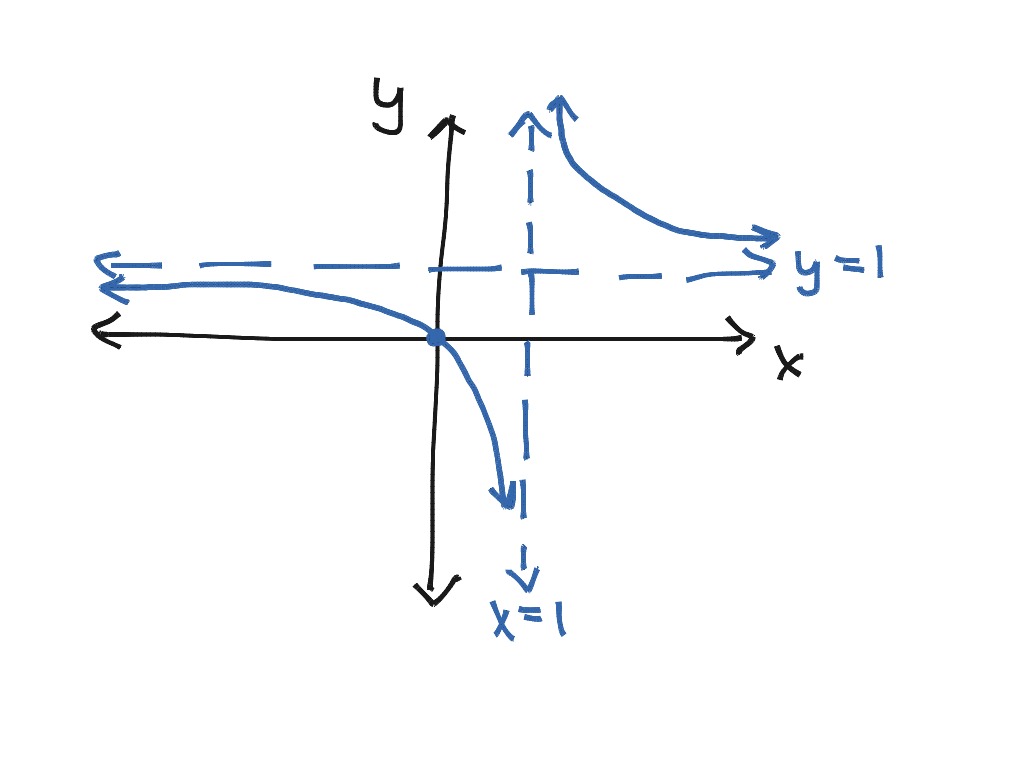
The domain of \(f\) is the entire real line; This notion is called the concavity of the function. This section deals with curves which are not polynomials.

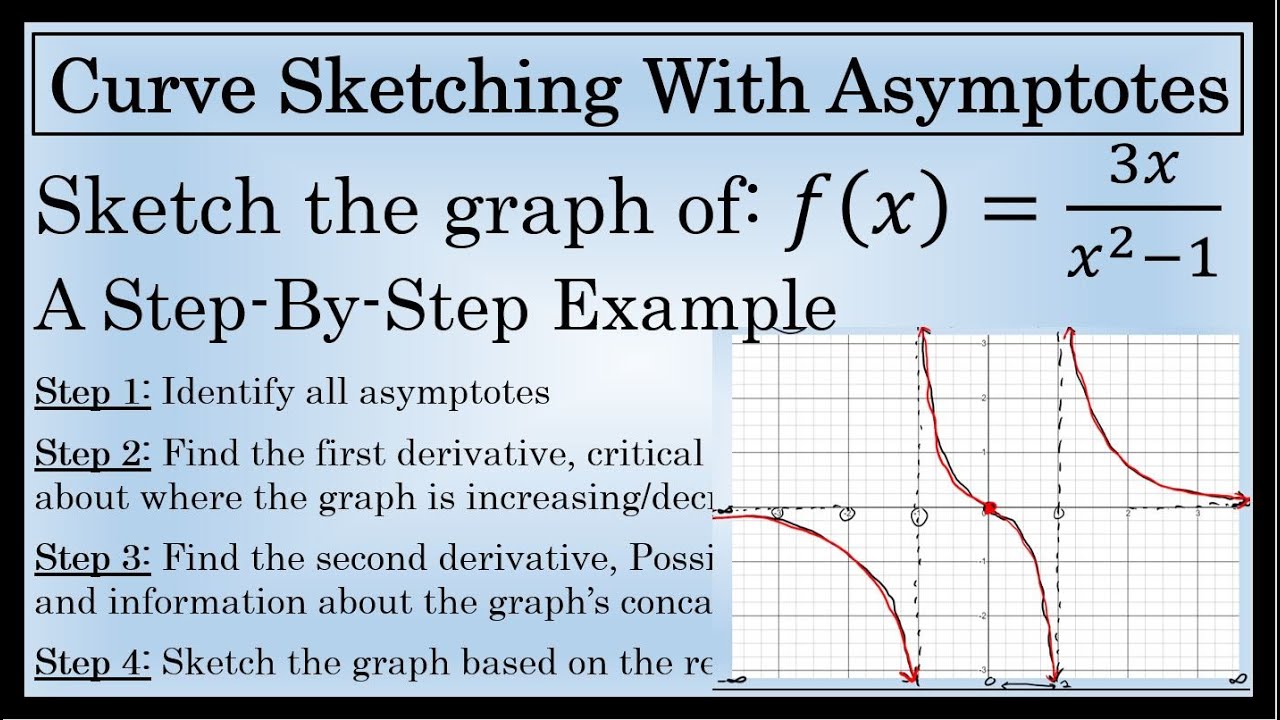
We now have enough analytical tools to draw graphs of a wide variety of algebraic and transcendental functions. The following steps are taken in the process of curve sketching: It is an application of the theory of curves to find their main features.

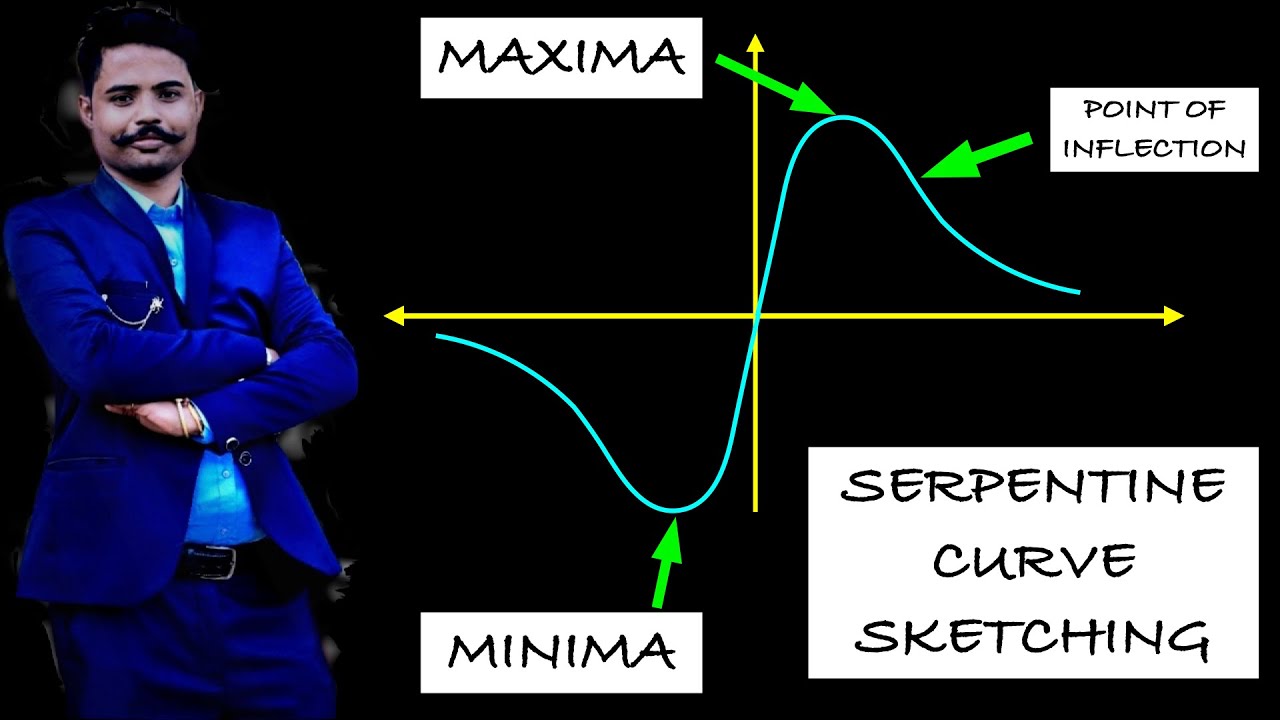
This insightful guide offers a comprehensive overview from understanding basic principles to exploring advanced techniques. Are you ready to take your understanding of calculus to the next level? Curve sketching shows us how we can understand and predict the behavior of the function based on its first and second derivatives.

Curve sketching is the process of using algebra and calculus to find the features of a function and then plotting those features in order to draw the function on a. They're just like local extreme, but they're gonna be important to identify when we're curve sketching because again, we want to break up the graph of the function into regions. Discover the role of curve sketching in creating.

Approximation and curve sketching part b: Conic section is a curve obtained by the intersection of the surface of a cone with a plane. In each case in the above figure the function is increasing, so that f ′ (x) > 0, but the manner in which the function increases is determined by its concavity, that is, by the sign of the second derivative f ″ (x).

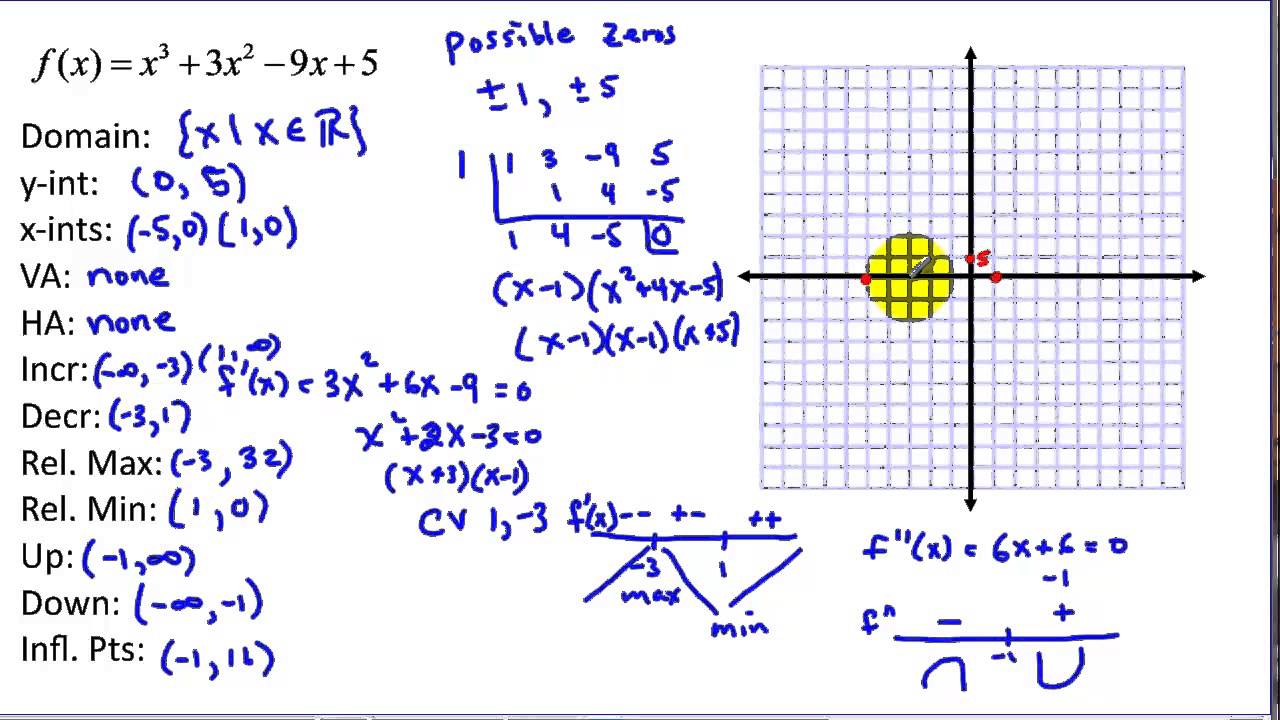
If the graph curves, does it curve upward or curve downward? Before showing how to graph specific functions, let’s look at a. Analyze and sketch a graph using the curve sketching process and using the first and second derivative tests to find extrema and concavity.

In this article, you’ll see a list of the 10 key characteristics that describe a graph. It turns out, quite a lot! More on curve sketching using differentiation.

What can calculus tell us about curve sketching? To sketch the graph of f(x), you will. Functions and their graphs are important not only in math but in other fields and applications as well.

Look no further than curve sketching, a fundamental concept that is essential for mastering applications of derivatives. Curve sketching is important as it helps us visualize and understand properties and behavior of any. In geometry, curve sketching (or curve tracing) are techniques for producing a rough idea of overall shape of a plane curve given its equation, without computing the large numbers of points required for a detailed plot.