Have A Tips About What Is Curve Smoothing Mean And Standard Deviation Graph In Excel

Smooth the data using a window with requested size.
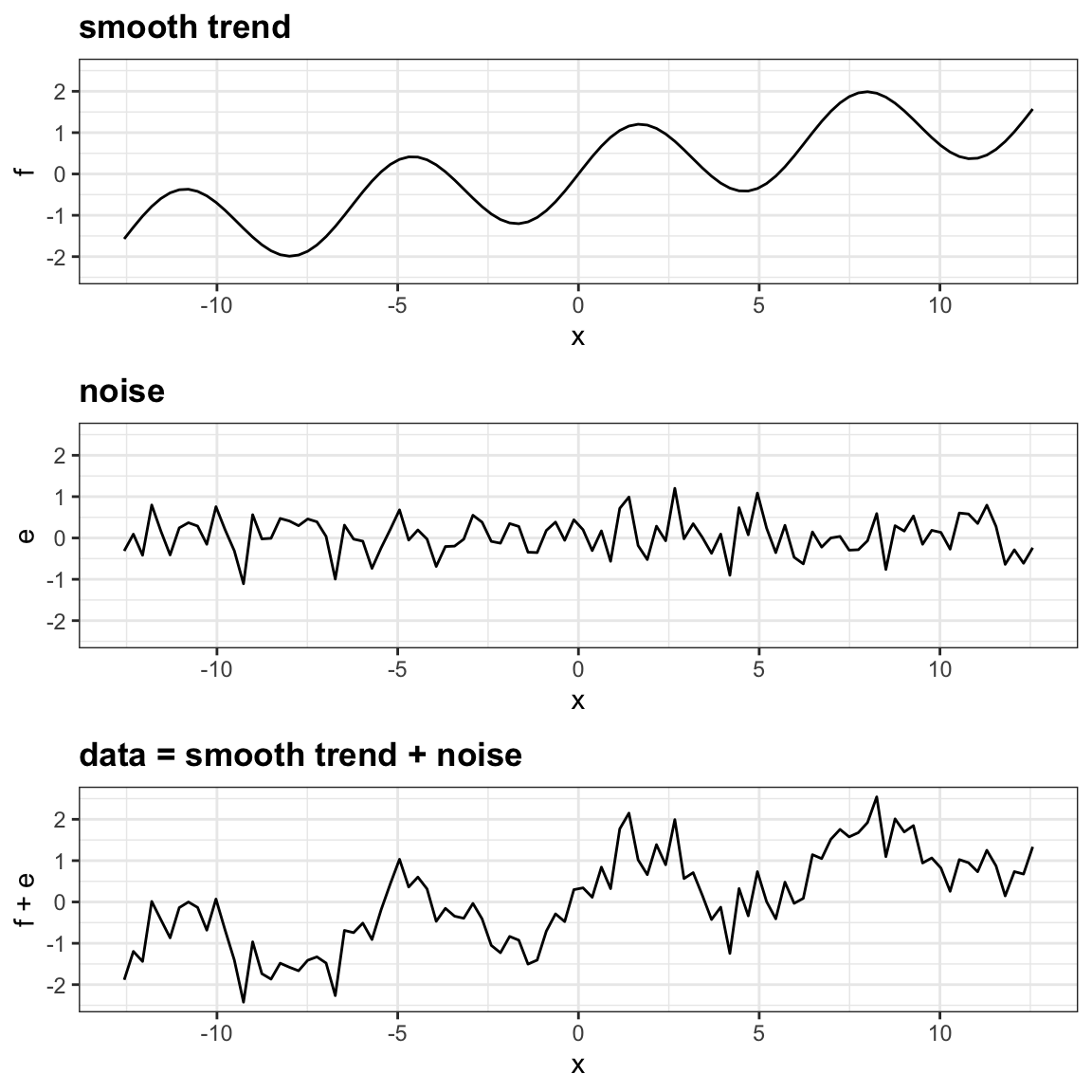
What is curve smoothing. Y_lowess = sm.nonparametric.lowess(list_y, list_x, frac = 0.30) # 30 % lowess smoothing. It is designed to detect trends in the presence of noisy data in cases in which the shape of the trend is unknown. Other names given to this technique are curve fitting and low pass filtering.
Let's examine the curves $\mathbf{r}_1(t) = \langle t,t\rangle$ and $\mathbf{r}_2(t) = \langle t^3,t^3\rangle$. A smoothed curve implies that the data goes places where it has not been measured. Smoothed lines without points are even worse, because the person trying to interpret the chart doesn’t even know what points on the smoothed curve belong there.
Data smoothing can be defined as a statistical approach of eliminating outliers from datasets to make the patterns more noticeable. Whether you choose the tighter (frac=0.12) or looser (frac=0.20) curve, either lowess curve here outshines all our previous attempts at smoothing the noisy data. The parameter df (degrees of freedom) controls the smoothness of the curve.
In keeping with the goals of the course, we will primarily focus on using the models for visualization and not attempt a detailed statistical analysis of when and. Smoothing algorithms are either global or local because they take data and filter out noise across the entire, global series, or over a smaller, local series by summarizing a local or global domain of y, resulting in an estimation of the underlying data called a smooth. I have some concerns regarding the second condition:
The only possible outcome is misinterpretation. A smooth curve is a curve which is a smooth function, where the word curve is interpreted in the analytic geometry context. A large df allows a very exible curve, e.g., a curve that can have multiple local maxima and minima.
In my experience it is simple to tune and often gives great results. So for instance in green's theorem, smoothness would mean the functions $l,m \in c^{(1)}$. I know there are many methods to fit a smooth curve but i'm not sure which one would be most appropriate for this type of curve and how you would write it in r.
The aim of smoothing is to give a general idea of relatively slow changes of value with little attention paid to the close matching of data values, while curve fitting concentrates on achieving as close a match as possible. In general, a smooth curve is a rectifiable curve created on an interval from a differentiable function. Smoothing is a very powerful technique used all across data analysis.
A clear definition of smoothing of a 1d signal from scipy cookbook shows you how it works. A moving average smoothes a series by consolidating the monthly data points into longer units of time—namely an average of several months’ data. Unfortunately, definitions found in many elementary calculus textbooks are often slightly ambiguous [2].
This (usually) has the effect of blurring the sharp edges in the smoothed data. In this paper, we review the statistical. In applications, when you say the curve is smooth it means till the derivatives you are interested in the curve has to be continuous.
# weight between 0 and 1. Randomized smoothing is a popular certified defense against adversarial attacks. Tilak mandadi is executive vice president, ventures and chief digital, data, analytics and technology officer at cvs health.

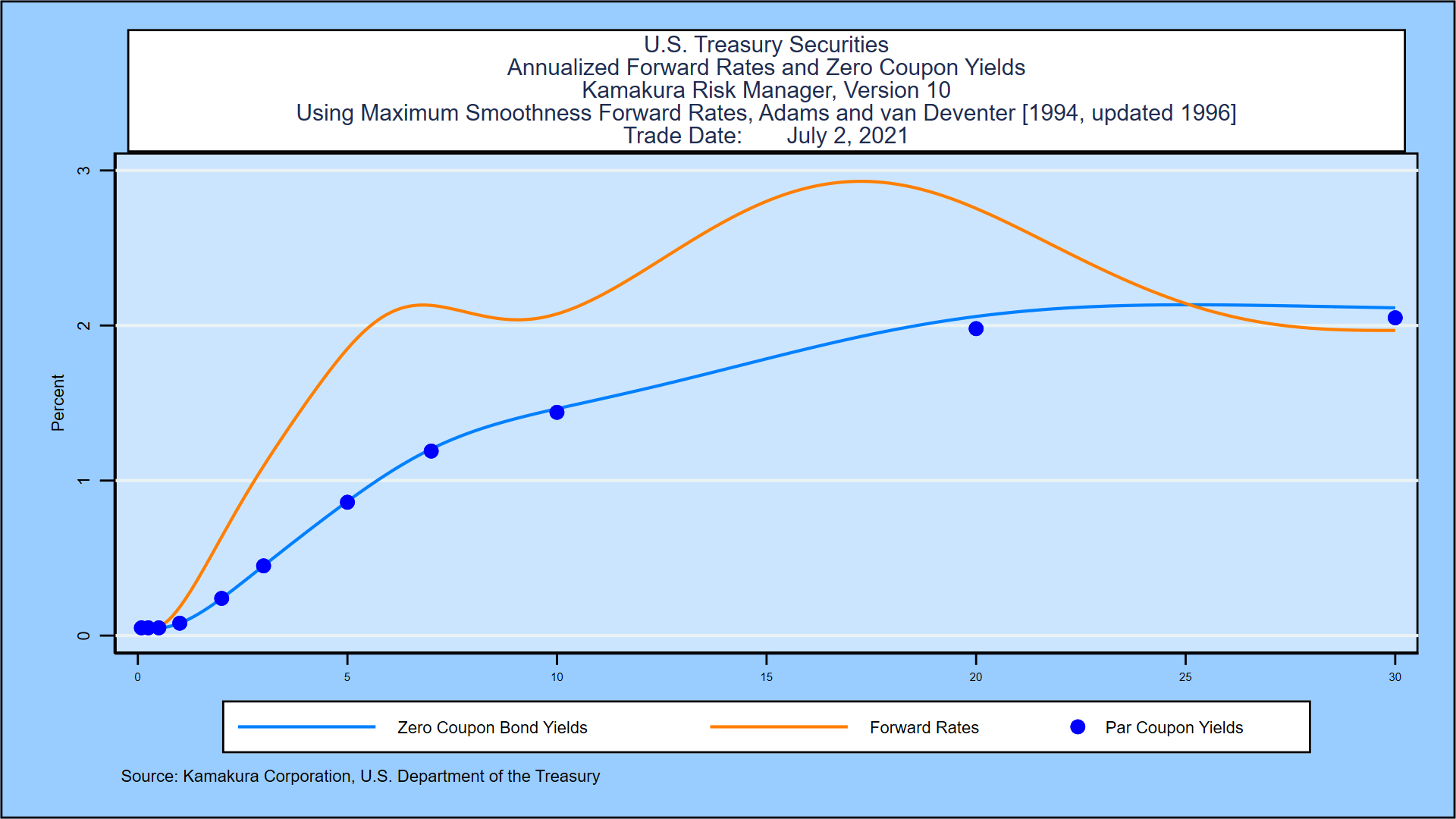








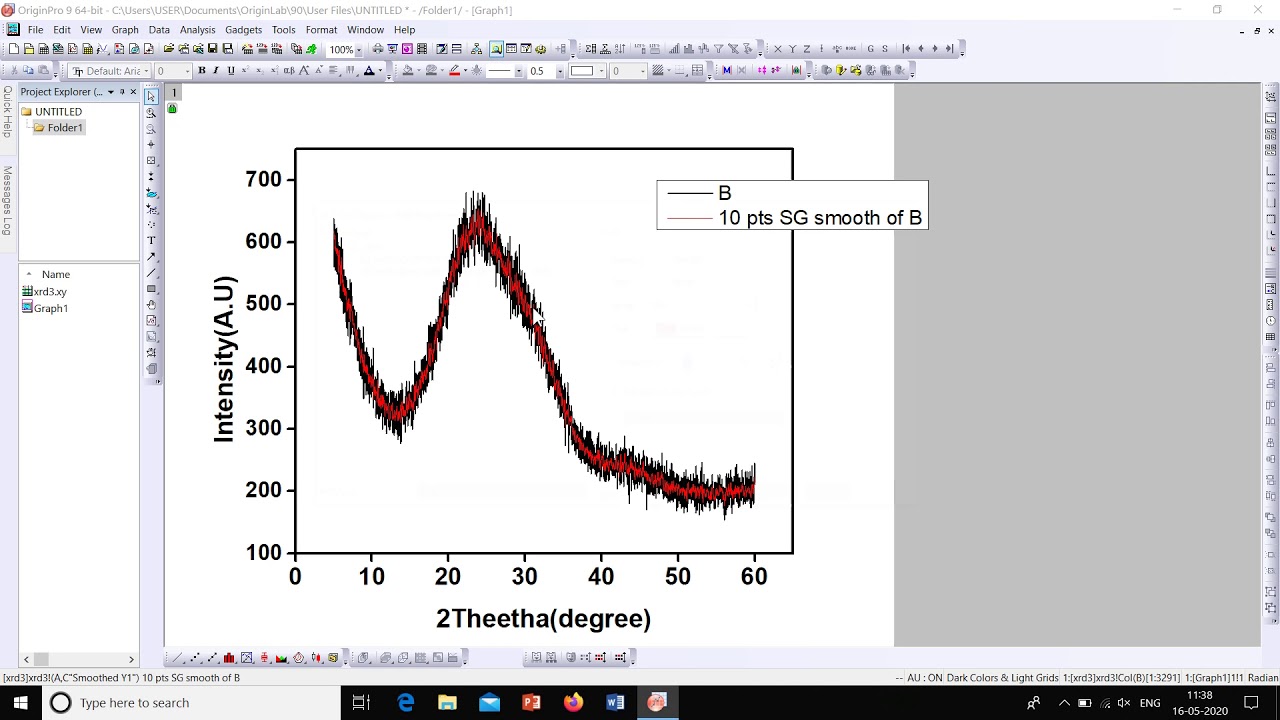




![[Math] Smoothing of a step function using smoothstep. (Curve fitting](https://i.stack.imgur.com/4zBDR.jpg)