Simple Tips About What Is A Hyperbola Curve Smooth Line Matlab

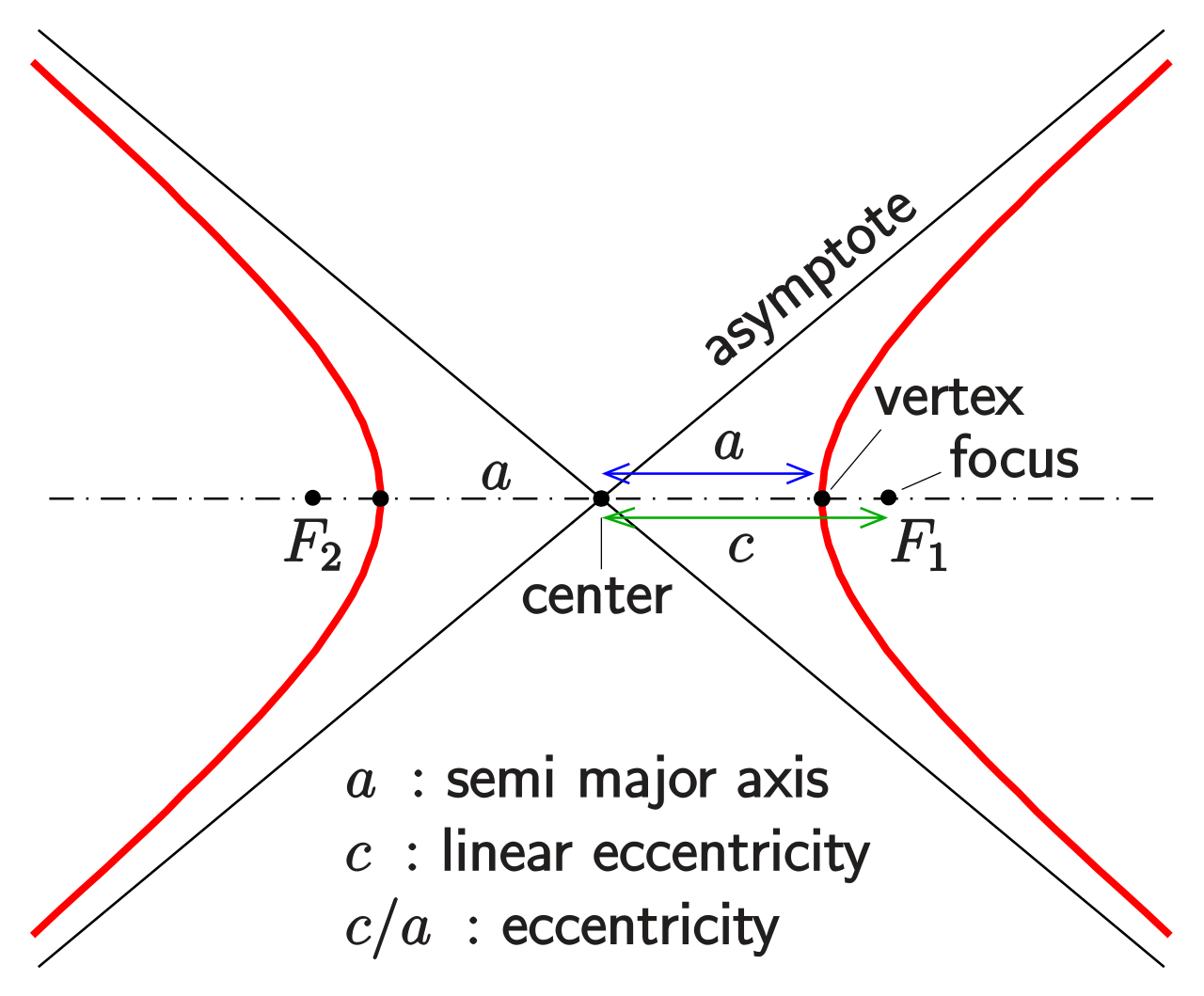
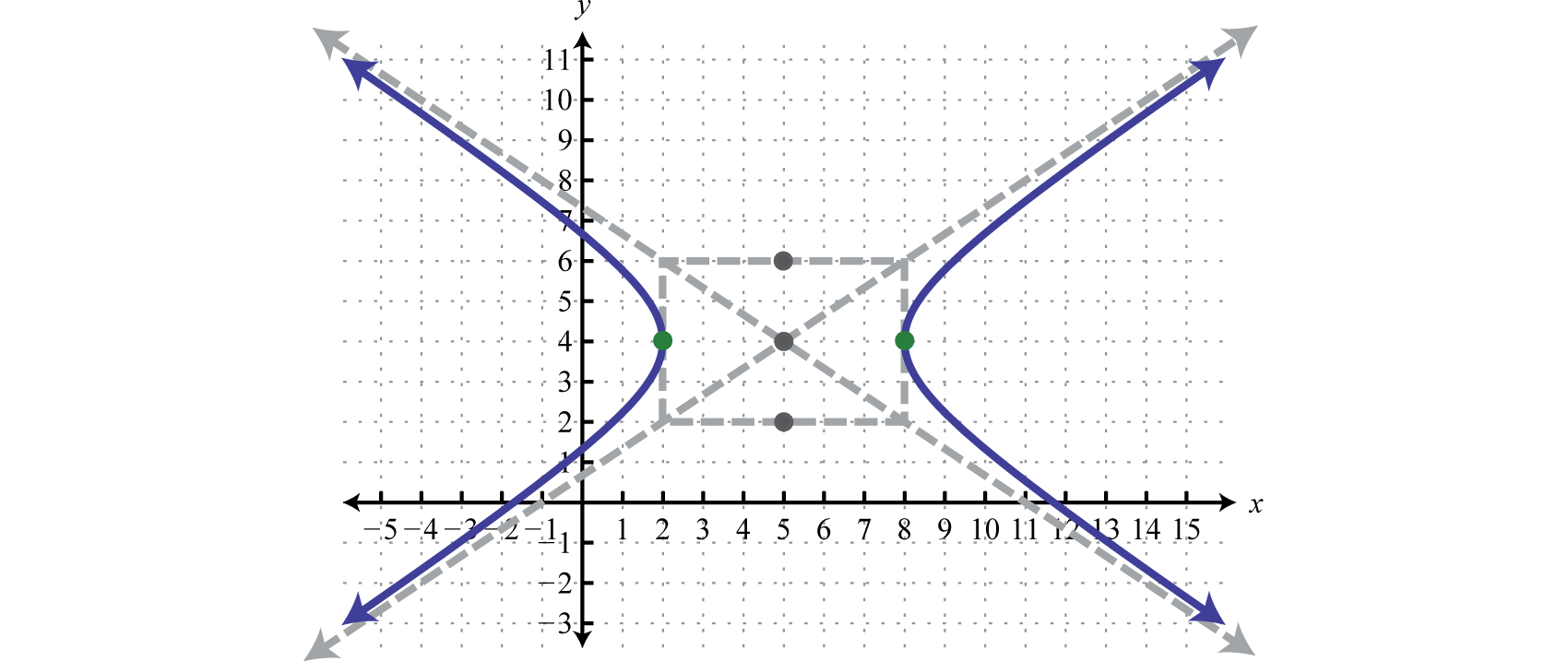
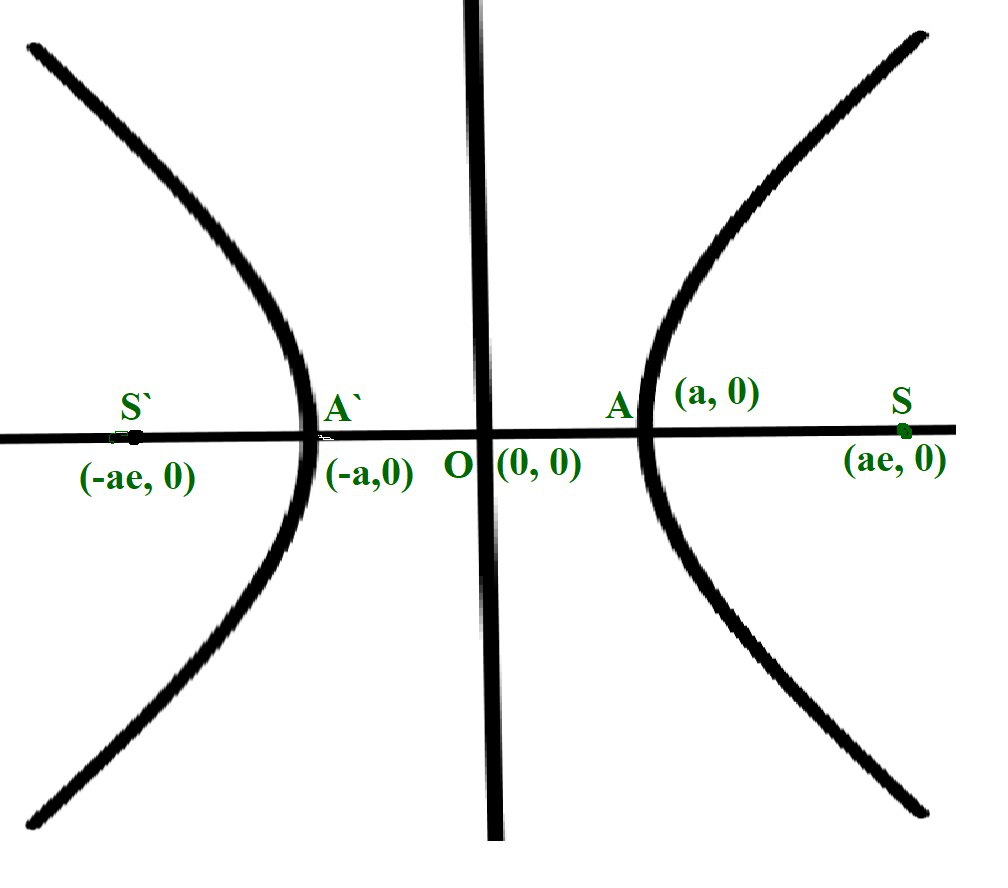
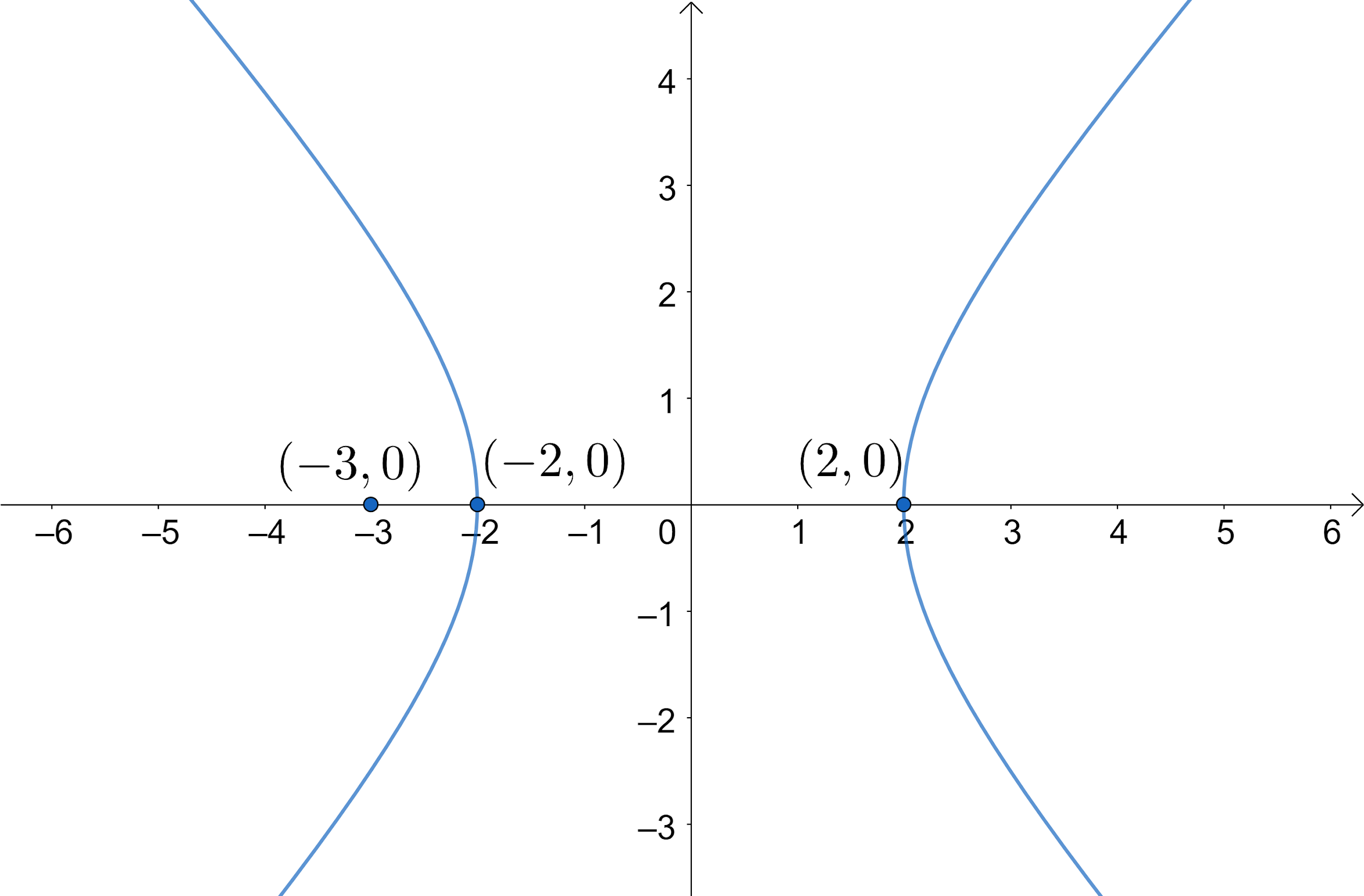
Points on the separate branches of the graph where the distance is at a minimum are called vertices 25.

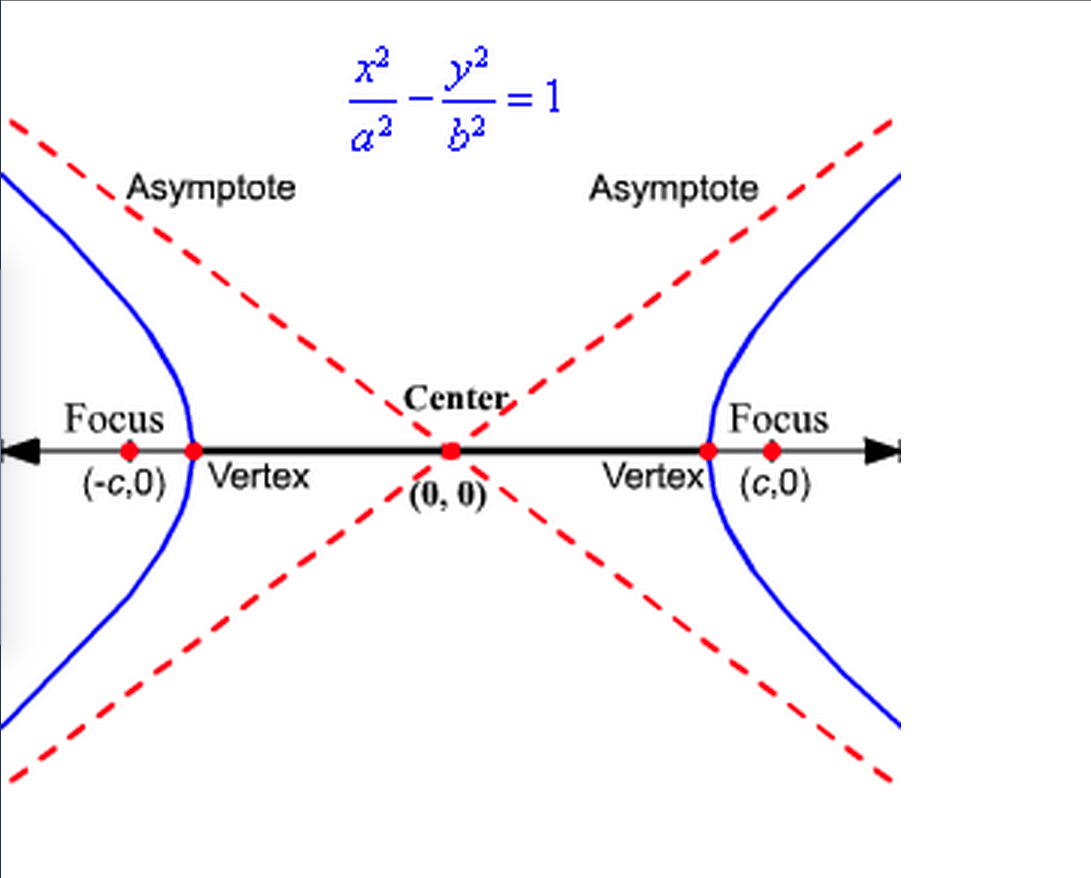
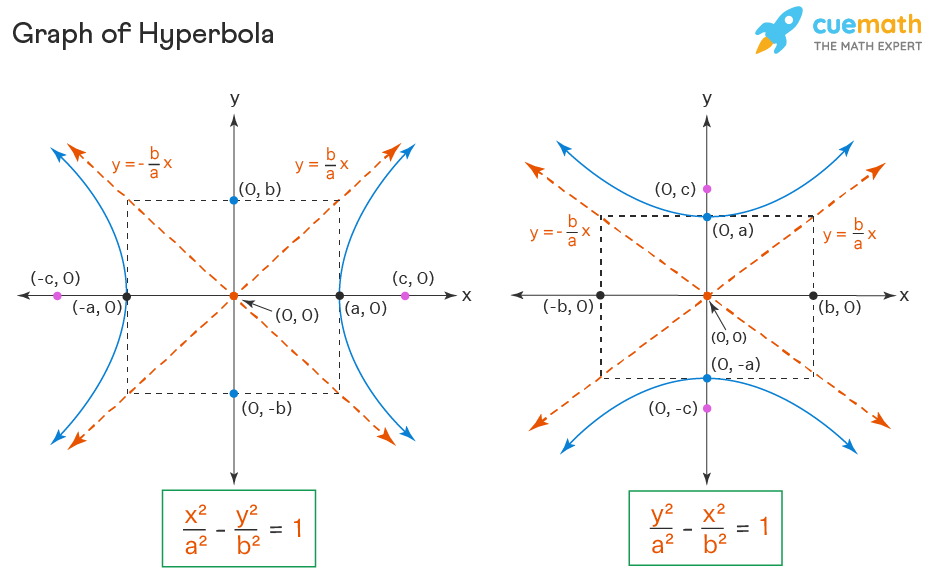
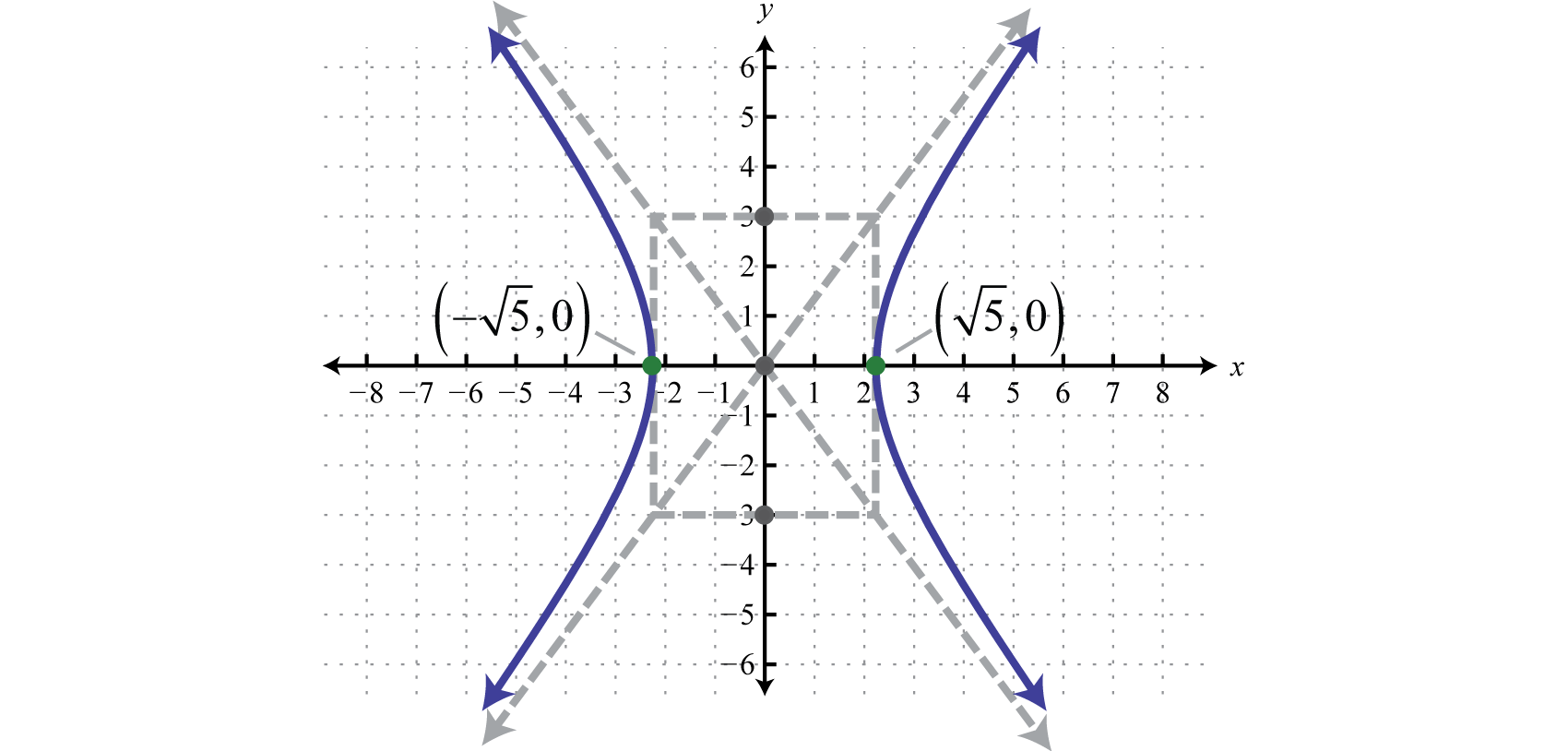
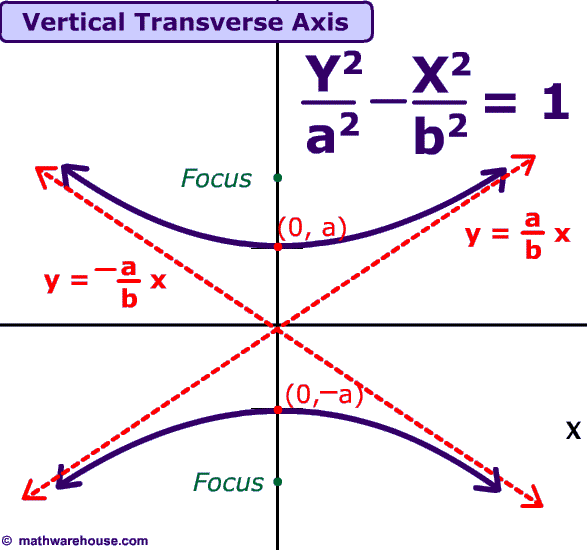
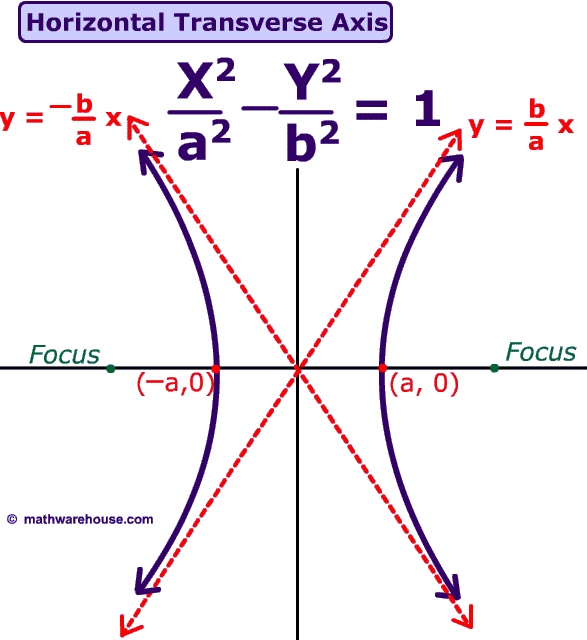
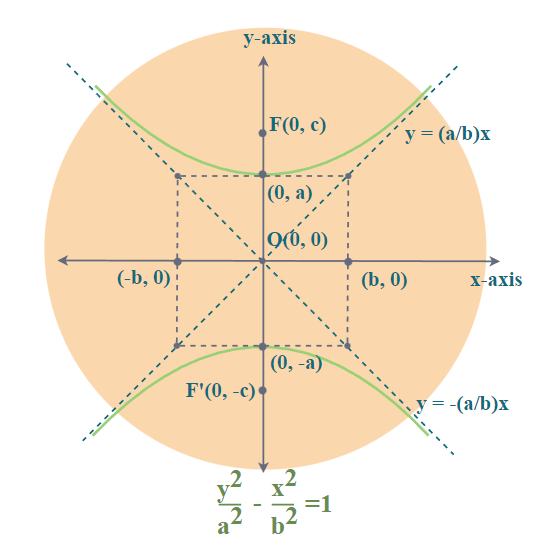
What is a hyperbola curve. It is a conic section formed by intersecting a right circular cone with a plane at an angle such that both halves of the cone are intersected. The transverse axis is the axis that crosses through both vertices and foci, and the conjugate axis is perpendicular to it. But in the case of the circle and ellipse, the curves are closed curves.

Locating the vertices and foci of a hyperbola. Here, we will study the hyperbola equation, foci, eccentricity, directrix, latus rectum and characteristics of such curves. In analytic geometry a hyperbola is a conic section formed by intersecting a right circular cone with a plane at an angle such that both halves of the cone are intersected.

In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Moreover, we show that the entropy of. Let $\mu$ be an ergodic harmonic measure on $\mathscr{f}$.

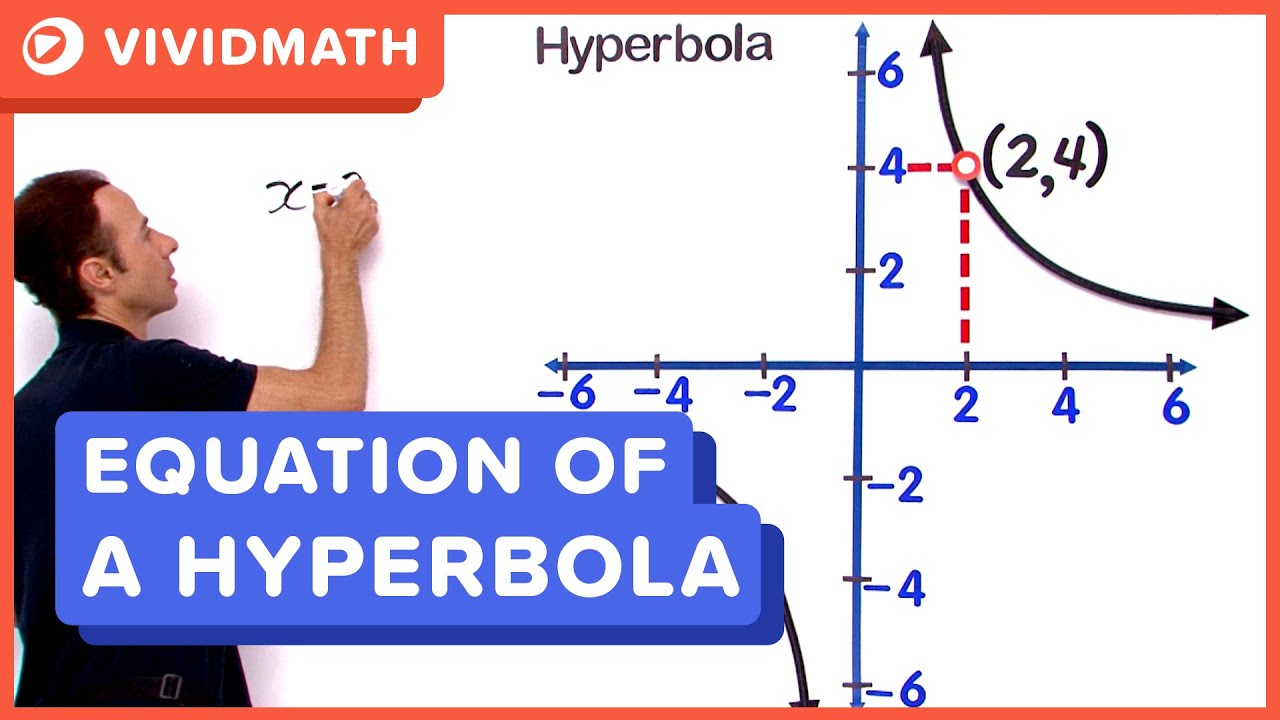
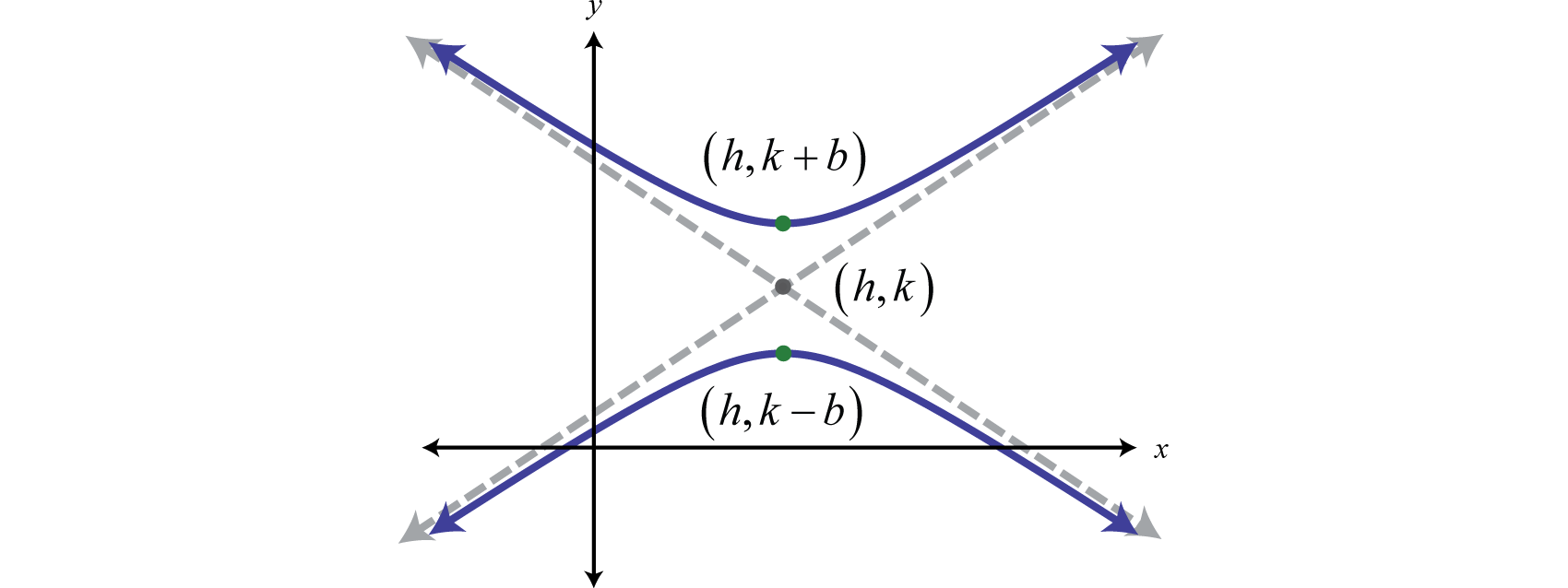
A hyperbola is a smooth curve in a plane with two branches that mirror each other, resembling two infinite bows. What is the hyperbola curve? In other words, the curve of the parabola and hyperbola does not end.

In analytic geometry, a hyperbola is a conic section formed by intersecting a right circular cone with a plane at an angle such that both halves of the cone are intersected. Both hyperbolas and parabolas are open curves; It will be shown in section 7.4 that the curve \(y=\frac{1}{x}\) is a hyperbola, which has two branches (see figure [fig:hyper1x]).

The hyperbola will be symmetrical regardless. Chen of the university of oxford is awarded the pólya prize for his deep research into nonlinear partial. Any branch of a hyperbola can also be defined as a curve where the distances of any point from:

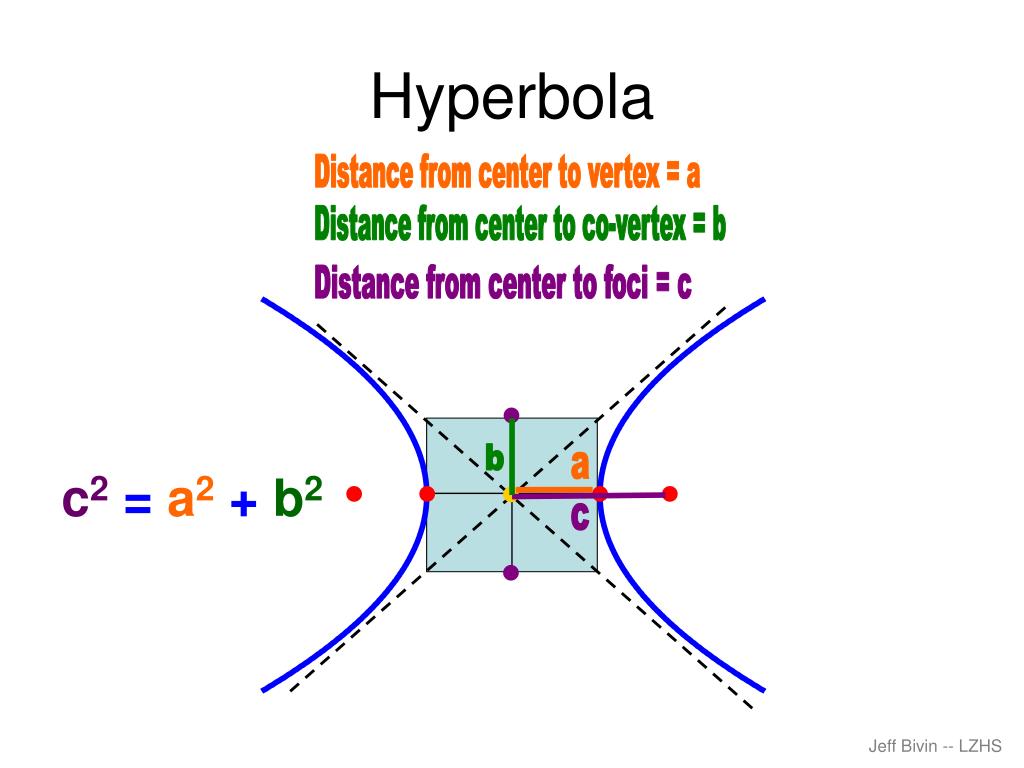
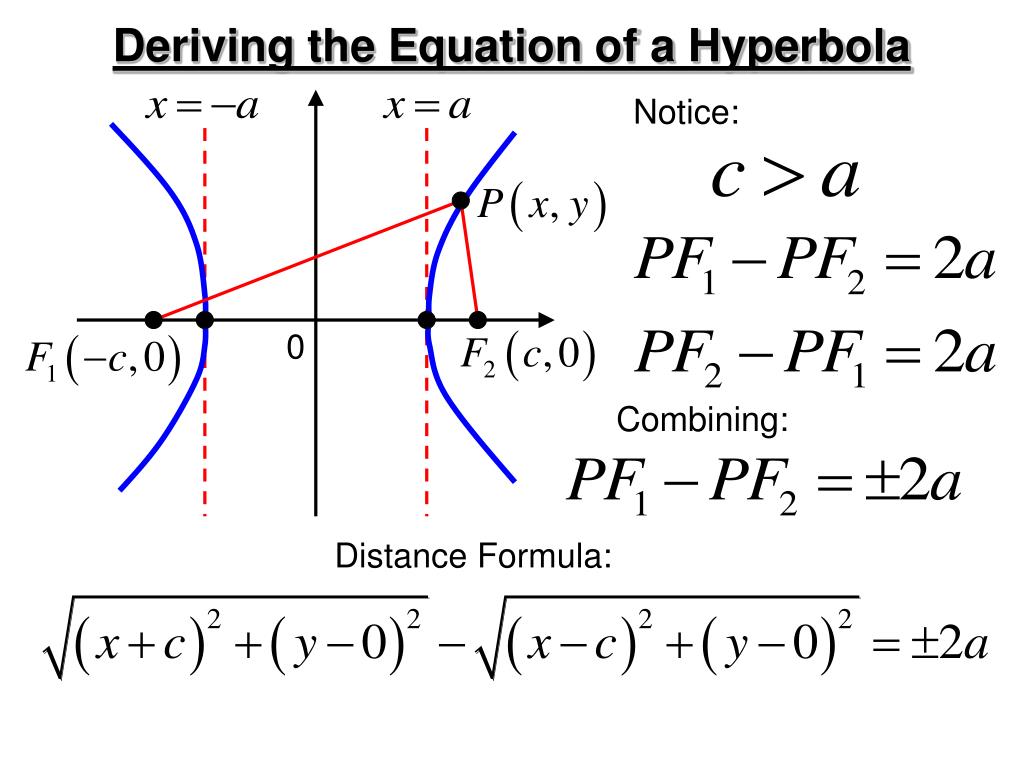
A hyperbola consists of two curves opening in opposite directions. (this means that a < c for hyperbolas.) this length x is called the focal parameter. As a plane curve it may be defined as the path (locus) of a point moving so that the ratio of the distance from a fixed point (the focus) to.

A fixed point (the focus), and; This intersection produces two separate unbounded curves that are mirror images of each other (figure \(\pageindex{2}\)). Hyperbolic / ˌ h aɪ p ər ˈ b ɒ l ɪ k / ⓘ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set.

Hanging cables form a curve called a catenary. The plane need not be parallel to the cone’s axis; The hyperbola is the shape of an orbit of a body on an escape trajectory (i.e., a body with positive energy), such as some comets, about a fixed mass, such as the sun.

Just like one of its conic partners, the ellipse, a hyperbola also has two foci and is defined as the set of points where the absolute value of the difference of the distances to the two foci is constant. A fixed straight line (the directrix) are always in the same ratio. This intersection produces two separate unbounded curves that are mirror images of each other.