Spectacular Tips About Can Curvature Be Negative Ggplot2 Geom_line

Now recall that κ1(p) κ 1 ( p) and κ2(p) κ 2 ( p) are the maximum and minimum normal curvatures of all curves passing through p.

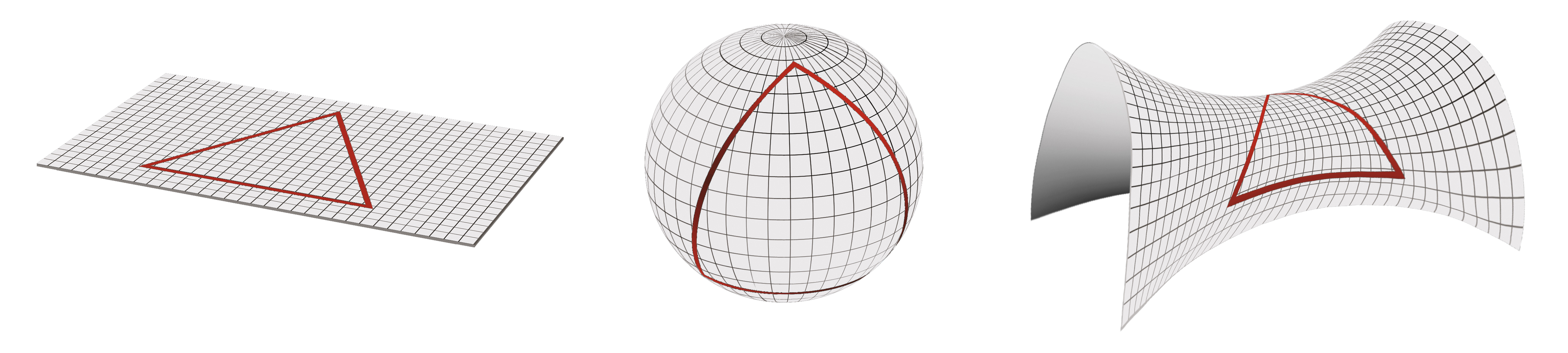
Can curvature be negative. In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. A space of constant negative curvature has a geometry called hyperbolic, and is of some interest because it appears to be the one that describes the spatial dimensions of our universe on a cosmological scale. Negative curvature, similarly, means the sum of the angles is less than 180 degrees.

You might think about what this means on a pringles potato chip! Gaussian curvature is an intrinsic measure of curvature, depending only on distances that are measured “within” or along the surface, not on the way it is isometrically embedded in euclidean space. A few examples of surfaces with both positive and negative gaussian curvature can be readily found in nature:

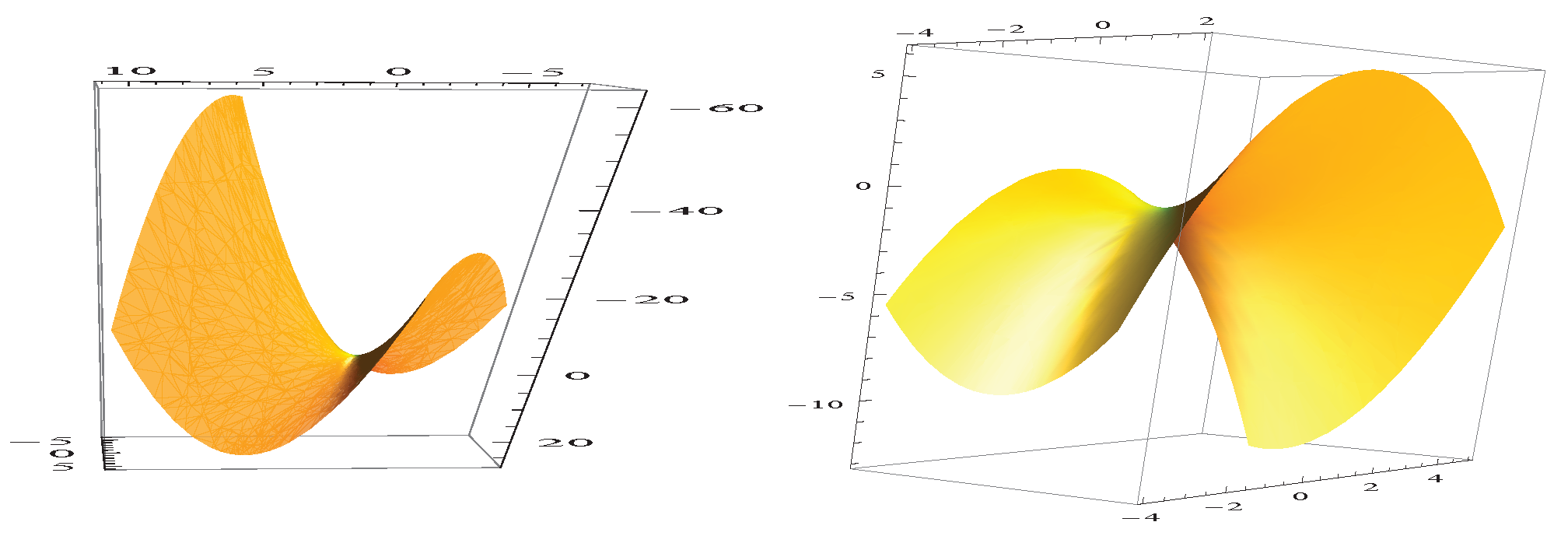
However, unlike a line, a surface (at each given point) can have either positive or negative curvature. In this case the actual structure is far from zero mean curvature exhibiting a constant and positive mean curvature. Namely, it is supposed to be negative.

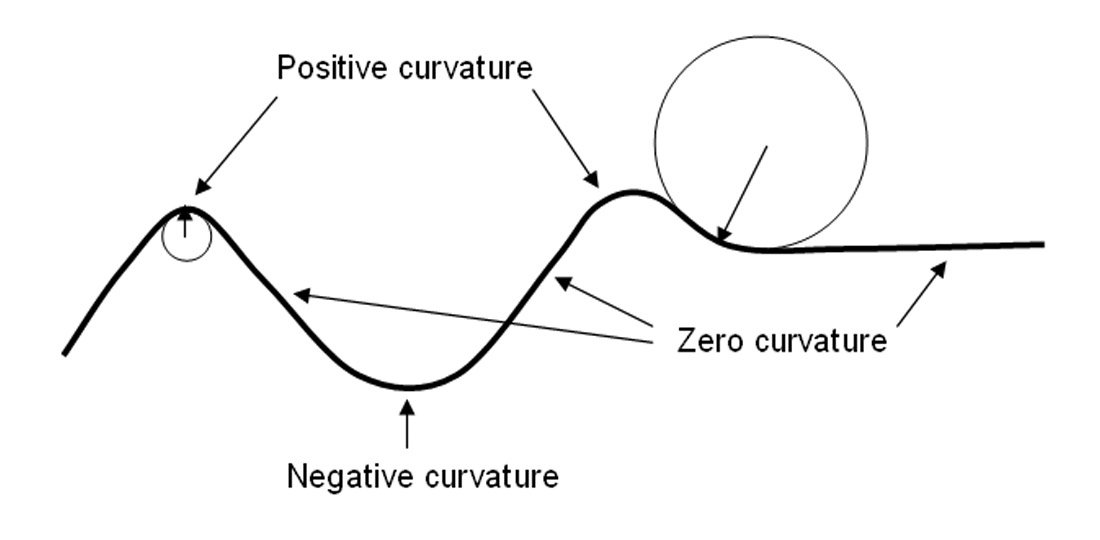
If a curve or surface is contained in a larger space, curvature can be defined extrinsically relative to the ambient space. If the slope is becoming less as you go to the right (as in figure 14), or as in figure 33, then, even though the curve may be going upward, since the change is such as to diminish its slope, its $\dfrac{d^2y}{dx^2}$ will be negative. It is positive if ${\bf t}$ turns counterclockwise, and negative if ${\bf t}$ turns clockwise when $s$ increases.

There are different forms of such surfaces, even of revolution, but the simplest is the surface called pseudosphere, which is formed by revolving a. This curvature has a sign: To find the curvature given the parametric function s → ‍ defining a curve:

To start with the simple case of a flat plane then the curvature at every point is zero. If the circumference is greater than 2πr and the area is greater than πr2 the surface has negative curvature. A surface has positive curvature at a point if the surface curves away from that point in the same direction relative to the tangent to the surface, regardless of the cutting plane.

A pear (usually), a peanut shell, a baseball bat (some negative gaussian curvature at the handle). The curvature is unchanged under a global rotation of $\gamma$, but changes its sign when $\gamma$ undergoes a reflection with respect to a line. If the circumference is less than 2πr and the area is less than πr2 the surface has positive curvature;

The curvature, denoted κ ‍ , is one divided by the radius of curvature. For k k to be zero, either κ1 = 0 κ 1 = 0 or κ2 = 0 κ 2 = 0. At greater depths, the correction factor is always positive due to the increased beam spread beyond the focal zone caused by the surface curvature.

Physically correction factor starts out negative because of the focusing effect of the curved surface. Here the curvature is understood in the usual way, as the curvature of the metric induced by the ambient space. A surface has positive curvature at a point if the surface lives entirely on one side of the tangent plane, at least near the point of interest.

(equicalent to an infinite diameter sphere) In this space, surfaces of negative curvature are convex; The gaussian curvature can also be negative, as in the case of a hyperboloid or the inside of a torus.